
数学IIIの「式と曲線」では様々な曲線を扱うが,現行の高等学校学習指導要領では,平面上の曲線に関して,媒介変数による表示と極座標による表示について,「描画においてはコンピュータなどを積極的に活用するものとする」とされている。また,次期の高等学校学習指導要領の数学Cでも「日常の事象や社会の事象などを数学的に捉え,コンピュータなどの情報機器を用いて曲線を表すなどして,媒介変数や極座標及び複素数平面の考えを問題解決に活用したり,解決の過程を振り返って事象の 数学的な特徴や他の事象との関係を考察したりすること」を求めている。このノートでは,Snap!を利用して,媒介変数表示や極座標表示された曲線を描画する方法を述べる。なお,実際の授業においてはSnap!の取り扱いに十分な時間がとれない場合は,以下の準備項目および弧度法による三角関数についてはあらかじめ作成したファイルを配付して行うのが時間の節約になる。
Snap!のx座標y座標をそのまま用いると,単位が1ドットなのでグラフの表示には不便である。そのため複数ドットを1単位とした座標を作り,それに合わせて「動き」カテゴリーのブロックの代わりになるものを作成する。最初に新しい変数unitを作る。
unitの値が座標単位になるが,この値は描こうとする曲線により変えていく。 ここでは,unitの値を30にする。
次に,新しい座標をunitの値を1単位として作る。もとの座標と区別するため,大文字のX,Yを使う。移動のブロックは次のようになる。

ここで,引数は数値をとり,初期値を0に設定している。詳しくは引数名を定義するときに詳細画面で以下のようにする。
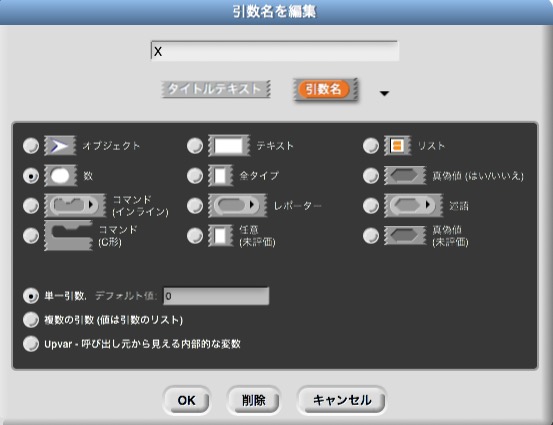
また,X座標の値をとるブロックを次のように作る。
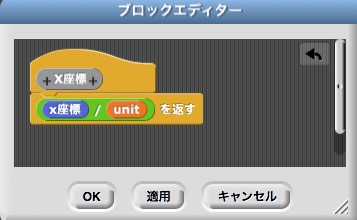
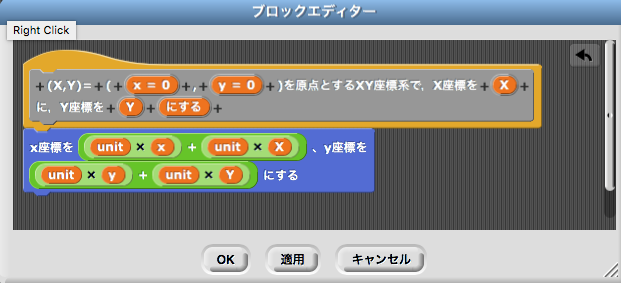
次に,座標の平行移動を行うことができるように,次のように平面上の任意の点を原点とする\(XY\)座標における点への移動を行うブロックを作成する。元の\(xy\)座標の原点を使用することが多いため,点のデフォルト値は\((0,0)\)をとるようにしている。
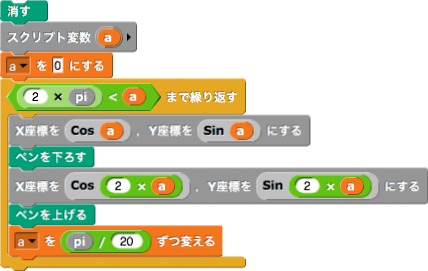
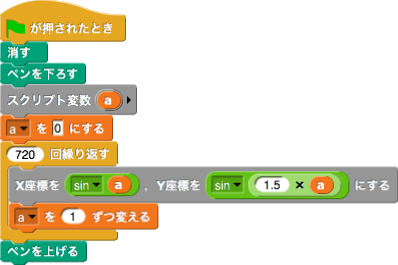
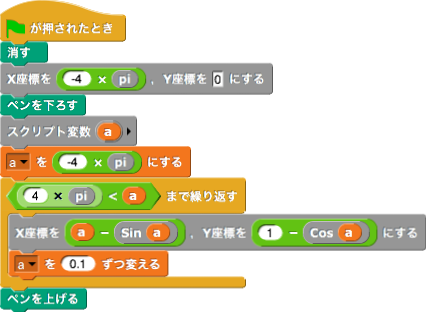
媒介変数で表示された関数,例えば\( X=f(t), Y=g(t)\)を描くには,\(t\)の値を少しずつ変えながら,\(X\)座標と\(Y\)座標を決めていけば,曲線のグラフが表示できる。例えば,リサージュ曲線(\( X=\sin a\theta , Y=\sin b\theta \))の一つである\(X=\sin \theta , Y=\sin \displaystyle\frac 32\theta\)を描くには次のようにすればよい。繰り返しの回数は\(\theta\)の係数により変わる。なお,Snap!の三角関数は引数が度数法の角度であることに注意する。
これを実行すると次が得られる。
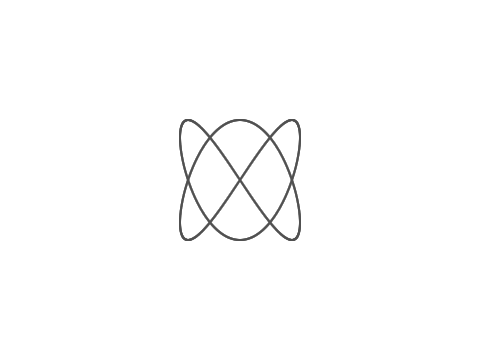
Snapの「演算」カテゴリーにある三角関数は,引数が度数法であるため,サイクロイドを描くには不便である。度数法から弧度法へ変換して行うこともできるが,javascriptで利用できる数学関数の三角関数は引数が弧度法であるため,これを利用する方法を考える。
Javascriptの数学関数はMathライブラリーにある。どのような関数が使えるかは,例えば, ここを見るとよい。例えば正弦関数(サイン)はMath.sin(x)で呼び出すことができる。また,円周率\(\pi\)はmath.PIで定義されているので,\(\pi\)の値を返すブロックは次のように作ることができる。
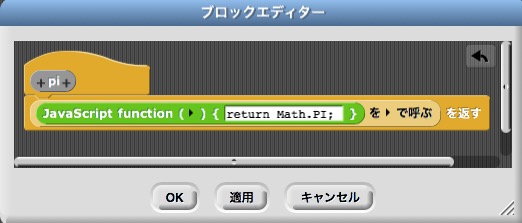
ここで,javascriptのプログラムは
return Math.PI;
の1行のみで,Math.PIの値を返すだけのプログラムである。
同じように三角関数も定義するが,三角関数は引数が必要なのでその部分も考慮する。 正弦関数(サイン)は次のようにブロックを定義する。
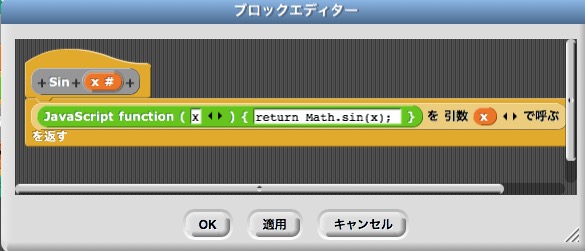
余弦関数(コサイン),正接関数(タンジェント)や逆三角関数も同じように定義する。
これらを用いてサイクロイド\(x=\theta-\sin\theta, y=1-\cos\theta\)を描くと次が得られる。

Snapでは極座標を表すブロックがないので,それを作る。ここで必要なのは,極座標の点\((r,\theta)\)を表す点への移動である。\(x=r\cos\theta,y=r\sin\theta\)の関係があることと\(\theta\)は弧度法の角であることをふまえ,ブロックを作る。 また,極方程式を考えるときは,\(r<0\)のときは,\((|r|,\theta +\pi)\)の点を表すことにも留意する。
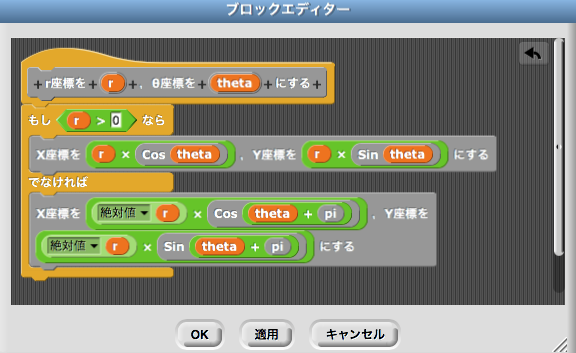
これを用いて,アルキメデスの渦巻き線(\(r=\displaystyle\frac 1{\ 2\ }\theta\))を描くと次のようになる。
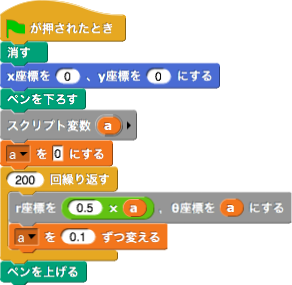

数研出版発行高等学校数学科用教科書数学IIIの80ページにある「ミルクティーを照らす光」というタイトルのコラムに次のような記述がある。(以下引用,図は省略)
媒介変数\(\theta\)を用いて表された半径\(1\)の円\(x=\cos\theta , y=\sin\theta\)を考える。この円上の2点\((\cos\theta, \sin\theta )\)と\((\cos 2\theta ,\sin 2\theta )\)を結ぶ線分を,\(0\)から\(2\pi \)まで\(\theta \)動かして複数個描くと,下の図[1]のようになる。また,円上の2点\((\cos\theta, \sin\theta )\)と\((\cos 3\theta ,\sin 3\theta )\)を結ぶ線分を,\(0\)から\(2\pi \)まで\(\theta \)動かして複数個描くと,下の図[2]のようになり,73ページの例12のOPを直径とする円を,\(-\frac{\pi}2\)から\(\frac{\pi}2\)まで\(\theta \)動かして複数個描くと,下の図[3]のようになる。いずれも,カージオイドのような図形が浮かび上がってくる。ここで73ページの例12とは,極方程式\(r=2a\cos\theta \)で表される円で,この円周上に点P\((2a\cos\theta, \theta)\)をとっている。
上記で引用されている図[1]と図[3]をSnap!を用いて描くと次のようになる。なお,図[3]では準備で作成した座標の平行移動を行うブロックを使用して作成している。
図[1]


図[3]
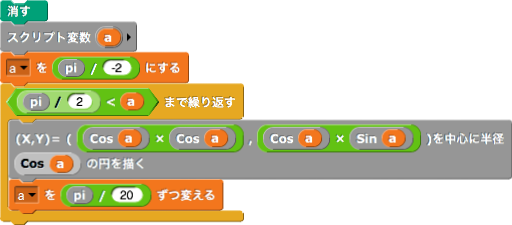

ブロック内で使用する「(x,y)=( , )を中心に半径 の円を描く」ブロックはどのように作成したらよいかは考えてみよ。