: 4 関係 : 3 集合族 : 3.1 集合族とは
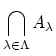 で表す.
で表す.
また,集合族
![]() に対し,
に対し,
![]() のいずれかの元となるようなものの全体,
すなわち
のいずれかの元となるようなものの全体,
すなわち
![]() をみたす
をみたす![]() の全体を
の全体を
![]() の和集合とよび,
の和集合とよび,
![]() あるいは
あるいは
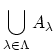 で表す.
で表す.
![]() を添字の集合とする集合族
を添字の集合とする集合族
![]() の場合は,
の場合は,
![$ \displaystyle \bigcup_{n=1}^{\infty}A_n , \displaystyle \bigcap_{n=1}^{\infty}A_n\rule[-20pt]{0pt}{8pt}$](img890.png) と表すこともある.
と表すこともある.
![]()
![$ \iff \forall b\in B [b\in \displaystyle \bigcap_{\lambda \in \Lambda}A_{\lambda} ]\strut$](img900.png)
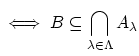
2:
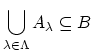
![$ \iff \forall b [ b\in \displaystyle \bigcup_{\lambda \in \Lambda}A_{\lambda} \rightarrow b \in B]\strut$](img903.png)
![]()
![]()
![]()
![]()
![]()
![$ \displaystyle \bigcup_{n=1}^{\infty}A_n =\mathbb{N}\rule[-20pt]{0pt}{8pt}$](img909.png) を示せ.
を示せ.
![$ \displaystyle \bigcup_{n=1}^{\infty}A_n =\mathbb{R}\rule[-20pt]{0pt}{8pt}$](img911.png) を示せ.
を示せ.
![$ A_n:=[0,\displaystyle\frac{1}{n}] , B_n:=(0,1+\displaystyle\frac{1}{n}),
C_n:=(-\displaystyle\frac{1}{n},n)\rule[-20pt]{0pt}{8pt}$](img919.png) とする.このとき,
とする.このとき,
![$ \displaystyle \bigcup_{n=1}^{\infty}A_n , \displaystyle
\bigcap_{n=1}^{\inft...
...}^{\infty}C_n ,
\displaystyle \bigcap_{n=1}^{\infty}C_n\rule[-20pt]{0pt}{8pt}$](img920.png) はどのような集合(区間)になるか調べよ.
はどのような集合(区間)になるか調べよ.
![$ A_n:=\{r\in \mathbb{R}\bigm \vert \vert r\vert\leqq \displaystyle\frac{1}{n}\}\rule[-20pt]{0pt}{8pt}$](img921.png) とおく.このとき,
とおく.このとき,
![$ \displaystyle \bigcap_{n=1}^{\infty}A_n =\{0\}\rule[-20pt]{0pt}{8pt}$](img922.png) を示せ.
を示せ.
![$ \displaystyle \bigcup_{n=1}^{\infty}A_n=\bigcup_{n=1}^{\infty}B_n\rule[-20pt]{0pt}{8pt}$](img925.png) であることを
示せ.
であることを
示せ.
![$ A_n:=\left\{ \left( \!\!\begin{array}{c} x y \end{array} \!\!\right)\rule[-...
...t} \rule[-16pt]{0.5pt}{39pt} x,y\in\mathbb{R},x^2+y^2\leqq n^2 \right\}\strut$](img928.png) とおく.このとき,
とおく.このとき,
![$ \displaystyle \bigcup_{n=1}^{\infty}A_n =\mathbb{R}^2\rule[-20pt]{0pt}{8pt}$](img929.png) を示せ.
を示せ.
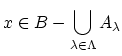
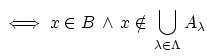
![]()
![]()
![]()
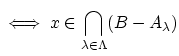
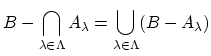 も同様に証明できる.
も同様に証明できる.
![]()
![]() のとき,
のとき,
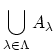 や
や
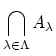 を
を
![]() ,
,
![]() と
表すことが多い.一般に
と
表すことが多い.一般に![]() が集合族であるとき,
が集合族であるとき,
TAKAHASHI Makoto : http://herb.h.kobe-u.ac.jp/