: 2.2 写像の合成(合成写像) : 2 写像 : 2 写像
![]() を集合とする.
を集合とする.![]() のひとつひとつの元に対し,
のひとつひとつの元に対し,![]() の元を一つ対応させる規則が定められていて,
その対応を記号
の元を一つ対応させる規則が定められていて,
その対応を記号![]() で表すとき,
で表すとき,![]() から
から![]() への写像(map)
への写像(map)![]() が与えられると言う.(
但し,対応が具体的な式で表される必要はない.)
が与えられると言う.(
但し,対応が具体的な式で表される必要はない.)
![]() や
や![]() が数の集合のとき,写像のことを関数(function)とよぶことが多い.
また扱う集合によって写像のことを作用素
とか変換あるいは演算とよぶこともある.
が数の集合のとき,写像のことを関数(function)とよぶことが多い.
また扱う集合によって写像のことを作用素
とか変換あるいは演算とよぶこともある.
![]() が
が![]() から
から![]() への写像であるとき,
への写像であるとき,
![]() で表し,
で表し,
![]() を
を![]() の定義域(domain)または始域と言い
の定義域(domain)または始域と言い
![]() で表す.
また,
で表す.
また,![]() を終域とよぶ.
写像
を終域とよぶ.
写像
![]() によって,
によって,![]() が
が
![]() に対応することを,
に対応することを,
![]() で表す.
このとき
で表す.
このとき![]() を
を![]() の
の![]() による像と言い
による像と言い
![]() であらわす.
上の例2.1の1の対応を
であらわす.
上の例2.1の1の対応を![]() で表すとき,
で表すとき,
![]() である.
従って
である.
従って
![]() `
`![]() の式' のような表現を与えると一つの写像(関数)が得られることになる
の式' のような表現を与えると一つの写像(関数)が得られることになる![]() .このように式を与えて写像を定義する場合,定義域が何であるかが不明であるが,一般に定義域が具体的に何も言及されていないときは,値の定義される元全体
を定義域と考えるのが普通である.
.このように式を与えて写像を定義する場合,定義域が何であるかが不明であるが,一般に定義域が具体的に何も言及されていないときは,値の定義される元全体
を定義域と考えるのが普通である.
![]() と
と![]() を
を![]() から
から![]() への写像とする.
への写像とする.![]() の任意の元
の任意の元![]() の
の![]() による像が一致するとき,
による像が一致するとき,
![]() と
と![]() は等しいと言い,
は等しいと言い,![]() で表す.
で表す.![]() から
から![]() への写像全体も集合である.
この集合を
への写像全体も集合である.
この集合を
![]() (あるいは
(あるいは![]() )で表す.
)で表す.
| 1 | 2 | 3 |
このような表の全体は
![]() 通りある.
通りある. ![]()
![]() を
を![]() の像(image)あるいは
の像(image)あるいは![]() の値域とよぶ.
の値域とよぶ.
![]() の値域を
の値域を
![]() あるいは
あるいは
![]() で表すこともある.
で表すこともある.
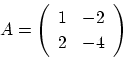 とする.このとき,
とする.このとき,
![]() であるから,
であるから,
![]() ならば
ならば
![]() である.
である.
2:
![]() であるから,1.より
であるから,1.より
![]() である.
よって,
である.
よって,
![]() である.逆に,
である.逆に,
![]() とすると,
とすると,
![]() となる
となる
![]() が存在する.このとき,
が存在する.このとき,![]() ならば
ならば
![]() であり,
であり,![]() ならば
ならば
![]() である.従って,いずれにしても
である.従って,いずれにしても
![]() が成り立つ.
が成り立つ.
3:
![]() であるから,1.より
であるから,1.より
![]() である.
よって,
である.
よって,
![]() である.
である.
![]()
![]() かつ
かつ
![]() とする.
とする.
![]() となる,
すなわち
となる,
すなわち
実数
![]() に対し,
に対し,![]() と
と![]() の間にある実数の集合を考える.このとき
の間にある実数の集合を考える.このとき![]() をその集合に含めるかどうかを考慮すると,
つぎのような4種類の集合を考えられる.
をその集合に含めるかどうかを考慮すると,
つぎのような4種類の集合を考えられる.
![]() の形の集合を閉区間とよび,
の形の集合を閉区間とよび,
![]() の形の集合を開区間とよぶ.
16
の形の集合を開区間とよぶ.
16
|
|
|
|
であるから,この区間では
![]() である.従って,
である.従って,
![]() である.また,
である.また,
![]() をみたす任意の
をみたす任意の![]() に対して,
に対して,
![]() とおくと
とおくと
![]() を
みたすから,
を
みたすから,
![]() も成り立つ.よって,
も成り立つ.よって,
![]() とする.
とする.
![]() に対し,その像が
に対し,その像が![]() に属するような
に属するような![]() の元全体を
の元全体を![]() の(
の(![]() に関する)
逆像(inverse image)とよび,
に関する)
逆像(inverse image)とよび,
![]() で表す.
で表す.
![]()
![]()
![]()
![]()
![]()
である. ![]()
![]()
2:
![]()
![]()
![]()
![]()
![]()
3: 演習問題
4:
![]()
![]()
![]()
![]()
![]()
5: 演習問題
![]()
TAKAHASHI Makoto : http://herb.h.kobe-u.ac.jp/