- ...の集合1
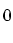 も自然数に入れる考え方もあるが,
このテキストでは
も自然数に入れる考え方もあるが,
このテキストでは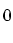 は自然数とは考えないことにする.
は自然数とは考えないことにする.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...たんしゅうごう@単集合(singleton)2
- singletonという語はコントラクトブリッジの用語
からきている.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...は同じ集合である3
-
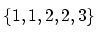 と
と
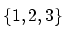 を区別して考えたい場合もある.このような
区別を考える集合を多重集合(multiset,bag)とよぶ.
を区別して考えたい場合もある.このような
区別を考える集合を多重集合(multiset,bag)とよぶ.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...についての条件4
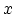 についての条件とは,おおざっぱにいうと
についての条件とは,おおざっぱにいうと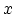 が具体的に与えられたときに真偽が決まるものであるが,“条件”とは何かということをきちんとここで述べることはしない.
例えば[4]を参考にしてほしい.
が具体的に与えられたときに真偽が決まるものであるが,“条件”とは何かということをきちんとここで述べることはしない.
例えば[4]を参考にしてほしい.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
であるから5
- ふたつの条件
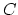 と
と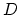 が必要十分条件の関係にあるとき,
が必要十分条件の関係にあるとき,
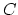 と
と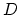 は同値であると言い,
は同値であると言い,
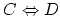 ,
,
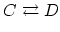 ,
あるいは
,
あるいは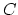 iff
iff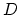 で表す.(iff はif and only if の略)
で表す.(iff はif and only if の略)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...と表すこともある
6
- このテキストではこの省略はしないが,他の文献では省略することもあるので注意して欲しい.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
で表す7
- 文献などでは単に
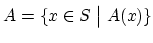 と書いて表すことが多いが,二つの集合が等しいことを表す
と書いて表すことが多いが,二つの集合が等しいことを表す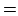 と区別するために
この記号法はここでは使わないことにする.
と区別するために
この記号法はここでは使わないことにする.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...りょうかきごう@量化記号(quantifier)8
- quantifierの訳語は定まっていない.量化記号のほかに量化子,量記号,限量子,限量記号などが使われる.しかし,口に出して言うときは,quantifierと原語でよばれることが多い.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
混乱する恐れがあるときは,この記号の書き換えを行って表現を変える事が多い9
- このように本質的では
ない変数記号の書き換えを計算機科学では“変数の
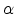 -変換”とよぶ.
-変換”とよぶ.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...ほうがんしゅうごう@包含集合10
- ここではsupersetの訳として包含集合を用いているが,これはここだけの用語で特に定まったものはない.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...おいらーず@オイラー図11
- オイラー図で書くことで視覚的にわかりやすくなるが,これに
たよりすぎるのは危険である.あくまで思考の補助手段と考えよう.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...を仮定して矛盾を導く12
-
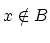 を背理法の仮定とよんで,本来の仮定である
を背理法の仮定とよんで,本来の仮定である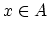 と区別する.
と区別する.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...で表すことにする13
- 集合
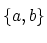 と
と
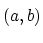 は全く異なるものである.
は全く異なるものである.
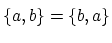 であるが,
一般に
であるが,
一般に
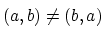 である.
である.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
により定義14
- 記号
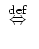 はこの左に
書かれたものが,右に書いたものにより定義されることを表す.
はこの左に
書かれたものが,右に書いたものにより定義されることを表す.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...としても一般性を失わわない15
-
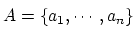 とすると一般的ではあるが,証明あるいは証明の表現が
複雑になるだけで本質的には
とすると一般的ではあるが,証明あるいは証明の表現が
複雑になるだけで本質的には
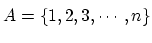 の場合を証明すれば,
一般の場合の証明は再現できる.このようなとき,“・・・としても一般性は
失わない”あるいは“一般性を失わずに・・・とできる”といって,
特殊な場合のみを証明することがある.もちろん,一般性を失わないことが
自明でない場合には,そのように特別な場合に制限してもよいことの証明が
必要である.
の場合を証明すれば,
一般の場合の証明は再現できる.このようなとき,“・・・としても一般性は
失わない”あるいは“一般性を失わずに・・・とできる”といって,
特殊な場合のみを証明することがある.もちろん,一般性を失わないことが
自明でない場合には,そのように特別な場合に制限してもよいことの証明が
必要である.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...かいくかん@開区間とよぶ.
16
-
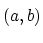 という表現は座標を表すものと同じであるが,開区間
という表現は座標を表すものと同じであるが,開区間
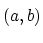 は集合であり,
座標
は集合であり,
座標
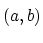 は平面上の点を表しているので注意が必要である.
は平面上の点を表しているので注意が必要である.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...が定義できる17
- 実際には
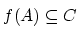 であれば
であれば
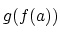 は定義できる.
は定義できる.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...で表す18
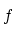 による原像を表すときも,同じ
による原像を表すときも,同じ
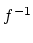 の記号を用いるので注意が必要である.但し,
の記号を用いるので注意が必要である.但し,
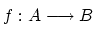 が全単射のときは,任意の
が全単射のときは,任意の
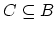 に対し,
に対し,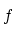 による
による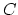 の原像
の原像
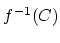 と
逆写像
と
逆写像
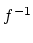 による
による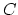 の像
の像
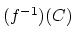 は一致する.
は一致する.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...を添字の集合とする集合族とよぶ
19
-
すべての集合族が
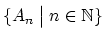 のように自然数の添字をつけて表されるならばわかりやすいのであるが,
自然数の添字では表されない集合族がある.例えば
のように自然数の添字をつけて表されるならばわかりやすいのであるが,
自然数の添字では表されない集合族がある.例えば
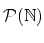 は
は
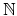 の
部分集合全体の集合族であるが,命題2.35からわかるように,この
の
部分集合全体の集合族であるが,命題2.35からわかるように,この
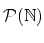 を
を
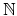 を添字の集合とする集合族
を添字の集合とする集合族
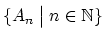 の形に表すことはできない.
の形に表すことはできない.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
代表元の取り方は,一意的には決まらない20
- 同値類に属する元はどれも代表元になれる.
どの元を用いてその同値類を表わすかということだけである.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.