: 4.3 商集合 : 4 関係 : 4.1 関係とは
R1:
![]() より
より![]() である.
である.
R2:
![]() とする.このとき,
とする.このとき,
![]() より,
より,
![]() であるから
であるから
![]() となる.
となる.
R3:
![]() とする.このとき,
とする.このとき,
![]() より,
より,
![]() であるから
であるから
![]() となる.
となる. ![]()
R1:
![]() を任意の整数とする.このとき,
を任意の整数とする.このとき,![]() より,
より,![]() は
は![]() で割り切れるから,
で割り切れるから,
![]() である.
である.
R2:
![]() を
を
![]() をみたす任意の整数とする.
をみたす任意の整数とする.![]() が
が![]() で割り切れるから,
で割り切れるから,
![]() を
を![]() で割ったときの商を
で割ったときの商を![]() とすると,
とすると,
![]() である.このとき,
である.このとき,
![]() であるから,
であるから,
![]() も
も![]() で割り切れる.よって,
で割り切れる.よって,
![]() である.
である.
R3:
![]() を
を
![]() かつ
かつ
![]() をみたす任意の整数とする.(2)と同様に,
をみたす任意の整数とする.(2)と同様に,
![]() を
を![]() で割ったときの商を
で割ったときの商を![]() ,
,![]() を
を![]() で割ったときの商を
で割ったときの商を![]() とすると,
とすると,
![]() である.
このとき,
である.
このとき,
![]() より,
より,![]() も
も![]() で割り切れる.よって,
で割り切れる.よって,![]() である.
である.
従って,![]() は条件R1,R2,R3をみたすから同値関係である.
は条件R1,R2,R3をみたすから同値関係である. ![]()
![]() ある番号
ある番号![]() が存在して,
が存在して,
![]() となる任意の
となる任意の![]() に対し,
に対し,
![]() である.
である.
![]() は同値関係であることを示せ.
は同値関係であることを示せ.
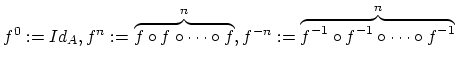 とする.
とする.
![]() をみたす正則な
をみたす正則な![]() 次行列
次行列![]() が存在する.
が存在する.
![]() は同値関係であることを示せ.
は同値関係であることを示せ.
2: 対偶を示す.
![]() とすると,
とすると,
![]() である
である![]() が存在する.このとき,
が存在する.このとき,
![]() であるから
であるから
![]() となる.
となる.
3: 任意の![]() に対し,
に対し,
![]() であるから,定理3.5より
であるから,定理3.5より
![$ \displaystyle \bigcup_{a \in A}[a]\subseteq A\strut$](img1058.png) は明らか.
は明らか.
![$ A \subseteq \displaystyle \bigcup_{a \in A}[a]\strut$](img1059.png) を示す.
を示す.![]() とする.
とする.
![]() であり,また
命題3.4より
であり,また
命題3.4より
![$ [x]\subseteq\displaystyle \bigcup_{a \in A}[a]\strut$](img1061.png) であるから,
であるから,
![$ x \in \displaystyle \bigcup_{a \in A}[a]\strut$](img1062.png) である.
である.
![]()
定理4.15より相異なる![]() を集めると,
を集めると,![]() を互いに共通部分のない部分集合で分割することになる.
を互いに共通部分のない部分集合で分割することになる.
![]() 上で定義された微分可能な関数の全体を
上で定義された微分可能な関数の全体を
![]() とする.
とする.
![]() 上の関係
上の関係![]() を
を
TAKAHASHI Makoto : http://herb.h.kobe-u.ac.jp/