: 1.3 部分集合と集合の相等 : 1 集合 : 1.1 集合とは
![]() 個の対象
個の対象
![]() が与えられたとき,それらを元としてもつ
集合を
が与えられたとき,それらを元としてもつ
集合を
![]() で表す.
で表す.
自然数![]() を元にもつ集合は
を元にもつ集合は
![]() と表され,式
と表され,式
![]() を元にもつ集合は
を元にもつ集合は
![]() と表される.
と表される.
この方法は元の個数が少ないときに有効である.有限でも元の数が多いときや無限にたくさんの 元をもつ集合に対して
と表すこともあるが,![]() の意味が文脈からはっきりしていることが必要である.
上の例では通常前者は
の意味が文脈からはっきりしていることが必要である.
上の例では通常前者は![]() から
から![]() までの自然数の集合,後者は正の偶数の集合であることが
予想される.
までの自然数の集合,後者は正の偶数の集合であることが
予想される.
![]() のみを元として持つ集合
のみを元として持つ集合
![]() を
を![]() のシングルトン ,単集合 (singleton)2とよぶ.
のシングルトン ,単集合 (singleton)2とよぶ.
![]() の中に同じ対象が複数あるとき,外延性の公理より,集合としては元の重複は考えない.例えば
の中に同じ対象が複数あるとき,外延性の公理より,集合としては元の重複は考えない.例えば
![]() と
と
![]() は同じ集合である3.
は同じ集合である3.
元![]() についての条件4
についての条件4
![]() が与えられたとき,
が与えられたとき,
![]() をみたすもの全体からなる集合
を
をみたすもの全体からなる集合
を
注意 ここでは条件
![]() に何の制限も付けていないが,
本当は
に何の制限も付けていないが,
本当は
![]() は何でもよいわけではない.詳しくは[5]などで,ラッセルのパラドックスについて調べてほしい.
は何でもよいわけではない.詳しくは[5]などで,ラッセルのパラドックスについて調べてほしい.
条件が'![]() かつ
かつ
![]() 'の形のときは,
'の形のときは,
![]() かつ
かつ
![]() を
を
![]() で表すことが多い.
例えば,例題1.4の集合は
で表すことが多い.
例えば,例題1.4の集合は
![]() のように表現する.
のように表現する.
条件を表すときに,日本語の“かつ”,“または”,“ならば”,“...でない”を用いると表現が複雑になる場合は,
論理記号
![]() を用いて表現することにする.
を用いて表現することにする.
“![]() は
は![]() 以下の自然数である”
という条件は,“
以下の自然数である”
という条件は,“
![]() ”と表現される.
”と表現される.
集合
![]() に
に![]() という名前をつけることを,
という名前をつけることを,
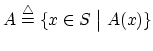 のように表すこともある.
のように表すこともある.
次の命題は当たり前のことであるが,重要である.
式
![]() が与えられたとき,
が与えられたとき,![]() の元
の元![]() に対する
に対する
![]() の値の全体を
の値の全体を
![]() で表す.
で表す.
![]() の正の倍数全体の集合は,自然数に
の正の倍数全体の集合は,自然数に![]() をかけてできる数の全体であるから,
をかけてできる数の全体であるから,
![]() のとき,定義より
のとき,定義より
となるから,
与えられた集合
![]() に対し,
に対し,
![]() を示すには,
を示すには,
![$ n=\dfrac{-1\pm 3\sqrt{5}}{2}\notin\strut \mathbb{Z}\rule[-20pt]{0pt}{8pt}$](img120.png) である.
よって,
である.
よって,
(*)の右辺の条件のように,“![]() となる(をみたす)
となる(をみたす)![]() が存在する”と条件が表されるとき
記号
が存在する”と条件が表されるとき
記号
![]() を用いて,
を用いて,
![]() のように表現する.
のように表現する.
(*)の右辺の条件をこの記号を用いて表現すると
となる.存在記号を用いて条件を表すときは
![]() のように,
存在している対象
のように,
存在している対象![]() の属する集合が明示される場合が
ほとんどである.この場合,板書などでは人により書き方は異なるが
の属する集合が明示される場合が
ほとんどである.この場合,板書などでは人により書き方は異なるが
|
|
|
|
|
|
|
|
|
|
|
|
|
|
のような表現が使われる.
![]() のように
のように
![]() が続くときは
が続くときは
![]() と省略する.
と省略する.
また(**)の右辺のように,
条件が“すべての![]() に対して,
に対して,![]() ”の形のときは,記号
”の形のときは,記号
![]() を用いて,
を用いて,
![]() のように表す.
のように表す.
また,
![]() の形の条件は,
の形の条件は,
|
|
|
|
|
|
|
|
|
|
のような表現が使われる.![]() の場合と異なり,
の場合と異なり,
![]() という使い方はしない.
という使い方はしない.
![]() のように
のように![]() が続くときは
が続くときは
![]() と省略する.このような表現法をもとにして,
と省略する.このような表現法をもとにして,
条件による集合の表現方法は変数が増えても同様である.
例えば,集合![]() の元
の元![]() と集合
と集合![]() の元
の元![]() についての式
についての式
![]() が与えられたとき,
が与えられたとき,
![]() の元
の元![]() と
と![]() の元
の元![]() によって
によって
![]() と表されるものの全体を
と表されるものの全体を
![]() で表す.
で表す.
![]() は
は
![]() と書くことにする.
と書くことにする.
実数上の![]() 項たてベクトル全体の集合
項たてベクトル全体の集合
![]() は
は
![$\displaystyle \left\{ \left( \!\!\begin{array}{c} a b \end{array} \!\!\right...
...[-20pt]{0pt}{8pt} \rule[-16pt]{0.5pt}{39pt} a,b \in \mathbb{R} \right\}\strut$](img167.png)
![$\displaystyle \left\{ \left(\begin{array}{cc}
a&b\\
c&d
\end{array}\right)\...
...le[-20pt]{0pt}{8pt} \rule[-16pt]{0.5pt}{39pt} a,b,c,d \in \mathbb{R} \right\}$](img169.png)
ベクトル
![]() と
と
![]() の一次結合全体の集合は
の一次結合全体の集合は
![$\displaystyle \left\{ x\left( \!\!\begin{array}{c} 1 2 \end{array} \!\!\righ...
...)\rule[-20pt]{0pt}{8pt} \rule[-16pt]{0.5pt}{39pt} x,y \in \mathbb{R} \right\}$](img171.png)
![]() のとき,
のとき,
与えられた集合
![]() に対し,
に対し,
![]() を示すには,
を示すには,
![]() となる元
となる元![]() と
と![]() が存在することを示せば良い.
が存在することを示せば良い.
また
![]() の左右の式を否定して書き換えると
の左右の式を否定して書き換えると
![$ \left( \!\!\begin{array}{c} 1 -1 \end{array} \!\!\right)\rule[-20pt]{0pt}{8...
...)\rule[-20pt]{0pt}{8pt} \rule[-16pt]{0.5pt}{39pt} x,y \in \mathbb{R} \right\}$](img215.png)
![$ \left( \begin{array}{c} 1 0 0 \end{array} \right)\in \left\{ x\left( \be...
...rule[-20pt]{0pt}{8pt} \rule[-16pt]{0.5pt}{39pt} x,y,z \in \mathbb{R} \right\}$](img216.png)
その1とその2の方法を組み合わせて集合を表現することもある.
例えば,集合![]() が条件
が条件
![]() により
1の方法を用いて
により
1の方法を用いて
![]() と表され,さらに集合
と表され,さらに集合![]() がその
がその![]() と式
と式
![]() を用いて2の
方法で
を用いて2の
方法で
![]() と表されている場合,
と表されている場合,![]() を条件
を条件
![]() と式
と式
![]() を用いて直接
を用いて直接
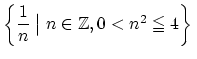
![]() のとき,
のとき,
与えられた集合
![]() に対し,
に対し,
![]() を示すには,
を示すには,
![]() かつ
かつ
![]() をみたす元
をみたす元![]() が存在することを示せば良い.
が存在することを示せば良い.
![]() の
の
![]() の左右の式を否定して書き換えると
の左右の式を否定して書き換えると
与えられた集合
![]() に対し,
に対し,
![]() を示すには,
を示すには,
ただし,
![]() をみたす
をみたす![]() が少ない場合
は前者の形で示す方が容易である.
が少ない場合
は前者の形で示す方が容易である.
変数が増えても同様に考える.
![]() のとき,
のとき,
![]() は条件
は条件
![]() をみたす
をみたす![]() の全体を表す集合であるから
記号
の全体を表す集合であるから
記号![]() を別の記号
を別の記号![]() で置き換えて
得られる表現
で置き換えて
得られる表現
![]() により定まる集合は
により定まる集合は![]() と同一の集合である.
と同一の集合である.
![]() と
と
![]() はともに
はともに![]() の倍数の
集合を表す.
の倍数の
集合を表す.
条件や集合をいくつも同時に扱うとき,条件を表す変数として同じ記号を用いると 混乱する恐れがあるときは,この記号の書き換えを行って表現を変える事が多い9.
TAKAHASHI Makoto : http://herb.h.kobe-u.ac.jp/