1.3 部分集合と集合の相等

1.3.1 部分集合

２つの集合$A,B$について$A$の元がすべて$B$の元になるとき，すなわち 任意の$x\in A$に対して$x\in B$ となるとき，$A$を$B$の部分集合(subset)とよび， $A\subseteq B$（あるいは $A \subseteqq B$）で表す．また，$A$が$B$の部分集合でないことは $A\nsubseteq B$で表す． $A\subseteq B$のとき，$B$を$A$の包含集合(superset)¹⁰とよぶ． $A\subseteq C$かつ $B\subseteq C$であることを， $A,B\subseteq C$で表す．同様に $A\subseteq B$かつ $A\subseteq C$であることを， $A\subseteq B,C$で表す．

部分集合の記号として$\subset$を用いる人や文献もあるが， $\subset$を後で述べる 真部分集合のことであると定義する場合もあるので，$\subset$の記号を用いている場合はここでいう部分集合をさすのか それとも真部分集合をさすのか注意する必要がある．

部分集合を表すのに，記号$\subset$を最初に用いたのはErnst Schrer(1841-1902)である． [7]

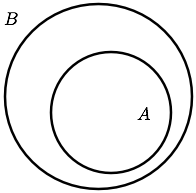
集合を平面上の閉じた曲線で囲む部分を用いて，集合をその囲まれた内部の点の集まりで表現するものを オイラー図¹¹(Euler Diagrams)とよぶ． 例えば，集合$B$とその部分集合$A$の関係はオイラー図で表すと次のようになる．

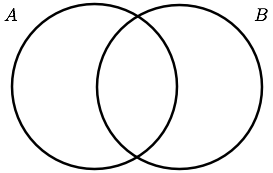
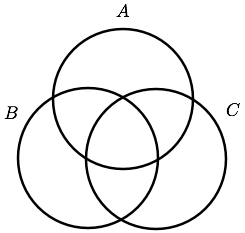
オイラー図と同様に一般的な集合の間の関係を表す表現として使われるものにベン図がある．扱う集合が２あるいは３個のときのベン図は以下のような集合を円で表した図になる．

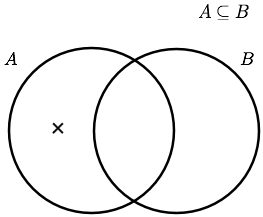
ベン図では，分割された領域に元がないことをその領域に×印を書いて表す．従って $A\subseteq B$をベン図を用いて表すと次のような図になる．

命題 1.28  

$A\subseteq B$かつ $B\subseteq C$ならば $A\subseteq C$

証明： オイラー図を書くと明らかであるが，定義に従って証明をする．

$A\subseteq B$かつ $B\subseteq C$とする．任意の$x\in A$に対して$x\in C$ となることを 示せばよい．$x\in A$とする． $A\subseteq B$より$x\in B$である．また $B\subseteq C$であるから $x\in C$となる． $\Box$

命題 1.29   $A:=\{x\bigm \vert P (x)\}\strut,B:=\{x\bigm \vert Q (x)\}\strut$とする．このとき， $A\subseteq B$であるための必要十分条件は $\forall x[P(x) \rightarrow Q(x)]\strut$ が成り立つことである．特に， $A:=\{x\in C\bigm \vert P (x)\}\strut$のときは $A\subseteq B$ であるための必要十分条件は $\forall x\in C [P(x) \rightarrow Q(x)]\strut$ が成り立つことである．

命題 1.30   $A:=\{q(x)\bigm \vert P (x)\}\strut$とする．このとき， $A\subseteq B$ であるための必要十分条件は $\forall x [P(x) \rightarrow q(x)\in B]\strut$ が成り立つことである． 特に， $B:=\{y \bigm \vert Q (y)\}\strut$のときは， $A\subseteq B$ であるための必要十分条件は $\forall x[P(x) \rightarrow Q(q(x))]\strut$ が成り立つことである．

命題 1.31   $A:=\{p(x)\bigm \vert x \in C\}\strut$とする．このとき， $A\subseteq B$ であるための必要十分条件は $\forall x \in C [p(x) \in B]\strut$ が成り立つことである．特に， $B:=\{q(y) \bigm \vert y \in D\}\strut$のときは， $A\subseteq B$ であるための必要十分条件は $\forall x \in C \exists y \in D[p(x)=q(y)]\strut$である．

命題1.30は変数が増えても同様である．

命題 1.32   $A:=\{p(x,y)\bigm \vert P (x,y)\}\strut$とする．このとき， $A\subseteq B$ であるための必要十分条件は $\forall x,y[P(x,y) \rightarrow p(x,y)\in B]\strut$ が成り立つことである． 特に， $B:=\{z \bigm \vert Q (z)\}\strut$のときは， $A\subseteq B$ であるための必要十分条件は $\forall x,y[P(x,y) \rightarrow Q(p(x,y))]\strut$ が成り立つことである．

     $A\subseteq B$を証明するには，定義より $x\in A \rightarrow x\in B$ を証明すれば良いのであるが，これを証明するには

1. $x\in A$を仮定して$x\in B$を導く以外に，
2. $x\notin\strut B$を仮定して $x\notin\strut A$を導いて対偶を示したり，
3. $x\in A$と $x\notin\strut B$を仮定して矛盾を導く¹²という背理法による証明が考えられる．

1,2,3のどの方針で証明するかは， 状況に応じて判断するしかないが，よくわからなければとりあえず3の方針で 考えるのが順当である．3は1,2に較べて仮定が多いので証明がしやすいという利点もある． 証明の方針が決まれば，そこから先は対象にしている理論の知識を用いて証明することが 必要になる．$A,B$が条件により表されているときは，命題1.29,1.30,1.31にあるような対応する命題を示せば良い．例えば $A:=\{x\bigm \vert P (x)\}\strut,B:=\{x\bigm \vert Q (x)\}\strut$のときは，以下のいずれかの証明をすればよい．

1. $P(x)\strut$を仮定して $Q(x)\strut$を導く．
2. $\neg Q(x)\strut$を仮定して $\neg P(x)\strut$を導く．
3. $P(x)\strut$と $\neg Q(x)\strut$を仮定して矛盾を導く．

また， $A:=\{x\in C\bigm \vert P (x)\}\strut B:=\{x\bigm \vert Q (x)\}\strut$の場合は

1. $x\in C$と $P(x)\strut$を仮定して $Q(x)\strut$を導く．
2. $x\in C$と $\neg Q(x)\strut$を仮定して $\neg P(x)\strut$を導く．
3. $x\in C$と $P(x)\strut$と $\neg Q(x)\strut$を仮定して矛盾を導く．

のいずれかの方法で証明をする． $A:=\{p(x)\bigm \vert x \in C\}\strut\subseteq B$の場合は

1. $x\in C$を仮定して $p(x)\in B\strut$を導く．
2. $p(x)\notin\strut B\strut$を仮定して $x\notin\strut C$を導く．
3. $x\in C$と $p(x)\notin\strut B\strut$を仮定して矛盾を導く．

を証明することになる．このタイプは非常によく現れる．ここでも写像の像に関する性質を示すときに出てくる． $A:=\{p(x)\bigm \vert P (x)\}\strut$と $B:=\{q(y)\bigm \vert Q (y)\}\strut$のときも同様であるが，この場合 $A\subseteq B$を示すためのポイントは， $p(x)\in B\strut$を示すこと，すなわち $p(x)\strut$の形のものを $q(y)\strut$の形で表現できるかどうかである．

例題 1.33   $\{x\in \mathbb{R}\bigm \vert -1\leqq x \leqq 1\}\strut\subseteq \{x \in \mathbb{R}\bigm \vert x^2-4 < 0\}\strut$を示せ．

解： 命題1.29より，任意の $x\in \mathbb{R}\strut$に対し，

$$-1\leqq x \leqq 1 \rightarrow x \in \mathbb{R} \wedge x^2-4 < 0$$

を示せばよいが，これは $x^2-4 < 0 \Leftrightarrow -2 < x < 2\strut$であるから常に成り立つ． $\Box$

問題 1.34   $\{x\in \mathbb{R}\bigm \vert x^3-x\geq 0\}\strut\subseteq \{x \in \mathbb{R}\bigm \vert x^3+x^2-x\geq 0\}\strut$を示せ．

例題 1.35   $\{n^2+n\bigm \vert n \in \mathbb{Z}\}\strut\subseteq \{2m\bigm \vert m \in \mathbb{Z}\}\strut$を示せ．

解： 命題1.30より，任意の $n\in \mathbb{Z}\strut$に対し，

$$n^2+n \in \{ 2m\bigm \vert n \in \mathbb{Z} \}\strut$$

が成り立つことを示せばよいが， $\{ 2m\bigm \vert n \in \mathbb{Z} \}\strut$は偶数の集合で， $n^2+n=n(n+1)\strut$より $n^2+n\strut$は偶数であるから成り立つ． $\Box$

例題 1.36   $\{6m+1\bigm \vert m \in \mathbb{Z}\}\strut\subseteq \{3n+1\bigm \vert n \in \mathbb{Z}\}\strut$を示せ．

解： 命題1.31より，任意の $m \in \mathbb{Z}\strut$に対し，

$$6m+1=3n+1$$

となる $n\in \mathbb{Z}\strut$が存在することを示せばよいが，これは明らかに$n=2m$ととればよい． $\Box$

問題 1.37   次を示せ．

1. $\{4n^2+4n+4 \bigm \vert n \in \mathbb{Z}\}\strut\subseteq \{m^2+3\bigm \vert m \in \mathbb{Z}\}\strut$
2. $\{9p^2+6p+2 \bigm \vert p \in \mathbb{Z}\}\strut\subseteq \{m^2+1\bigm \vert m \in \mathbb{Z}\}\strut$
3. $\{4n^2+6n+2 \bigm \vert n \in \mathbb{Z}\}\strut\subseteq \{m^2+m\bigm \vert m \in \mathbb{Z}\}\strut$
4. $\{m^2+m\bigm \vert m \in \mathbb{Z}\}\strut\subseteq \{4n^2+6n+2 \bigm \vert n \in \mathbb{Z}\}\strut$

例題 1.38   $\left\{ \left(\begin{array}{cc} 1&a\\ 0&1 \end{array}\right)\rule[-20pt]{0... ...le[-20pt]{0pt}{8pt}\subseteq\{ A\in M_2(\mathbb{R})\bigm \vert \det A=1\}\strut$を示せ．

解： 命題1.30より，任意の $a\in \mathbb{R}\strut$に対し，

$$\left(\begin{array}{cc} 1&a\\ 0&1 \end{array}\right)\in M_2(\... ...{cc} 1&a\\ 0&1 \end{array}\right)=1\rule[-20pt]{0pt}{8pt}\quad \textrm{(*)}$$

が成り立つことを示せばよい． $P=\left(\begin{array}{cc} 1&a\\ 0&1 \end{array}\right)\rule[-20pt]{0pt}{8pt}$は$2$次行列で $a\in \mathbb{R}\strut$であるから $P\in M_2(\mathbb{R})\strut$は明らか． また， $\det P=\left\vert\begin{array}{cc} 1&a\\ 0&1 \end{array}\right\vert =1-0=1\rule[-20pt]{0pt}{8pt}$であるから(*)が成り立つ． $\Box$

問題 1.39   $\left\{ \left(\begin{array}{cc} 1&-a\\ a+1&1 \end{array}\right)\rule[-20pt... ...\subseteq\{ A\in M_2(\mathbb{R})\bigm \vert \det A\ne 0\}\rule[-20pt]{0pt}{8pt}$を示せ．

命題1.29,1.30は考えている式や条件の変数が増えても同じように考えることができる．

    　 $A\subseteq B$の証明について詳しく述べたので， ついでに $A\nsubseteq B$の証明についても ふれておく．

$$A \subseteq B \iff \forall x \in A [x \in B]\strut$$

であるから $\Leftrightarrow$の左右の式を否定すると

$$A \nsubseteq B \iff \exists x \in A [ x \notin\strut B]$$

である．従って， $A\nsubseteq B$を証明するには，$A$の元であるが$B$の元ではない$x$が存在することを示せば良い．

例題 1.40   $\{2m\bigm \vert m \in \mathbb{Z}\}\strut\nsubseteq \{n^2+n \bigm \vert n \in \mathbb{Z}\}\strut$を示せ．

解： $4\in \{2m\bigm \vert m \in \mathbb{Z}\}\strut$である．一方， $n^2+n=n(n+1)\strut$は奇数と偶数の積であるから $4=n(n+1)\strut$となる $n\in \mathbb{Z}\strut$は存在しない．従って， $4\notin\strut \{n^2+n \bigm \vert n \in \mathbb{Z}\}\strut$である． よって， $\{2m\bigm \vert m \in \mathbb{Z}\}\strut\nsubseteq \{n^2+n \bigm \vert n \in \mathbb{Z}\}\strut$である． $\Box$

問題 1.41   $\{m^2+3\bigm \vert m \in \mathbb{Z}\}\strut\nsubseteq \{4n^2+4n+4 \bigm \vert n \in \mathbb{Z}\}\strut$を示せ．

実数の順序では， $a \nleqq b\strut$ならば $b < a\strut$であるが，集合の包含関係$\subseteq$ ではこれは成り立たないことに注意しよう． $A\nsubseteq B$でも， $B \subseteq A$とは限らない．

1.3.2 集合の相等

$A\subseteq B$かつ $B \subseteq A$ならば， $\forall x [x \in A \Leftrightarrow x \in B ]\strut$が成り立つから 外延性の公理より，$A=B$である． また $A\subseteq B \wedge A\ne B\strut$が成り立つとき，$A$は$B$の真部分集合であるといい， $A \subsetneqq B$で表す．

    $A=B$を証明するには， $A\subseteq B$と $B \subseteq A$ を証明すれば良いが，特に $A:=\{x\bigm \vert P (x)\}\strut$と $B:=\{x\bigm \vert Q (x)\}\strut$に対して $A=B$を示すには命題1.29より $P(x)\strut$と $Q(x)\strut$が$x$についての同値な条件であることを示せば良い． 一般的に$A=B$の証明の方針は次の(i),(ii)のどちらかである．

(i) $P(x)\strut$より同値変形を繰り返して $Q(x)\strut$を導く．

(ii) $P(x) \rightarrow Q(x)\strut$と $Q(x) \rightarrow P(x)\strut$に分けて，それぞれ証明する．

(ii)の場合は $A\subseteq B$と $B \subseteq A$をそれぞれ証明していることになる．

例題 1.42   $\{x^2+2 \bigm \vert x \in \mathbb{R}\}\strut$ $=$ $\{ x\in \mathbb{R}\bigm \vert x\geq 2 \}\strut$ を示せ．

解： $a \in \{x^2+2 \bigm \vert x \in \mathbb{R}\}\strut$

$\Leftrightarrow \exists x \in \mathbb{R}[a=x^2+2]\strut$

$\Leftrightarrow a\in \mathbb{R} \wedge a\geq 2\qquad (\because x^2 \geqq 0 (\forall x \in \mathbb{R}))\strut$

$\Leftrightarrow a \in \{ x\in \mathbb{R}\bigm \vert x\geq 2 \}\strut$ $\Box$

問題 1.43   次を示せ．

1. $\{\sin^2x +2\bigm \vert x \in \mathbb{R}\}\strut=\{ x\in \mathbb{R}\bigm \vert 2\leq x \leq 3 \}\strut$
2. $\{4n^2+6n+2 \bigm \vert n \in \mathbb{Z}\}\strut=\{m^2+m\bigm \vert m \in \mathbb{Z}\}\strut$

例題 1.44   $\boldsymbol{a}:=\left( \!\!\begin{array}{c} 1 2 \end{array} \!\!\right)\rul... ...\!\!\begin{array}{c} 2 1 \end{array} \!\!\right)\rule[-20pt]{0pt}{8pt}\strut$ $\in \mathbb{R}^2\strut$ とする．このとき

$$\{x\boldsymbol{a}+y\boldsymbol{b}\bigm \vert x,y\in \mathbb{R}\}\strut=\mathbb{R}^2$$

を示せ．

解： $\boldsymbol{a},\boldsymbol{b}\in \mathbb{R}^2\strut$より，任意の $x,y\in \mathbb{R}\strut$に対し $x\boldsymbol{a}+y\boldsymbol{b}\in \mathbb{R}^2\strut$である．従って， $\{x\boldsymbol{a}+y\boldsymbol{b}\bigm \vert x,y\in \mathbb{R}\}\strut\subseteq \mathbb{R}^2$ である．

逆に， $\boldsymbol{c}:=\left( \!\!\begin{array}{c} u v \end{array} \!\!\right)\rule[-20pt]{0pt}{8pt}\strut \in \mathbb{R}^2\strut$とする．２次行列 $A=[\boldsymbol{a},\boldsymbol{b}]\strut$ は

$$\det A =\left\vert\begin{array}{cc}1&2 2&1\end{array}\right\vert\rule[-20pt]{0pt}{8pt}= 1-4=-3 \ne 0$$

より正則であるから逆行列をもつ． $\left( \!\!\begin{array}{c} x y \end{array} \!\!\right)\rule[-20pt]{0pt}{8p... ...\!\!\begin{array}{c} u v \end{array} \!\!\right)\rule[-20pt]{0pt}{8pt}\strut$ とすると，

$$x\boldsymbol{a}+y\boldsymbol{b}\strut=A\left( \!\!\begin{array}{c... ...\!\!\begin{array}{c} u v \end{array} \!\!\right)\rule[-20pt]{0pt}{8pt}\strut$$

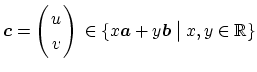となるから， $\boldsymbol{c}=\left( \!\!\begin{array}{c} u v \end{array} \!\!\right)\rule... ...8pt} \in \{x\boldsymbol{a}+y\boldsymbol{b}\bigm \vert x,y\in \mathbb{R}\}\strut$である．よって，

$$\mathbb{R}^2\subseteq \{x\boldsymbol{a}+y\boldsymbol{b}\bigm \vert x,y\in \mathbb{R}\}\strut$$

を得る． $\Box$

問題 1.45   $\left\{ x\left( \!\!\begin{array}{c} 1 2 \end{array} \!\!\right)\rule[-20pt... ...le[-20pt]{0pt}{8pt} \rule[-16pt]{0.5pt}{39pt} c \in \mathbb{R} \right\}\strut$を示せ．

問題 1.46   $\boldsymbol{a},\boldsymbol{b}\strut$を１次独立な $\mathbb{R}^2\strut$のベクトルとする．このとき

$$\{x\boldsymbol{a}+y\boldsymbol{b}\bigm \vert x,y\in \mathbb{R}\}\strut=\mathbb{R}^2$$

を示せ．（この問題は１次独立な平面上の二つのベクトルの一次結合全体は平面ベクトル全体と 一致することを示す問題である．）

問題 1.47   $a,b\strut$を互いに素な自然数とする．次の証明は$a$と$b$が互いに素な自然数ならば $ax+by=1\strut$をみたす整数$x,y$が存在することを用いて，

$$\{ma+nb\bigm \vert m,n\in \mathbb{Z}\}\strut=\mathbb{Z}$$

であることを示すものである．空白の中に適当な式または文をいれて証明を完成させよ．

$m,n,a,b\in \mathbb{Z}\strut$ならば， $\framebox[2.5cm]{\rm (1)} \in \mathbb{Z}\rule[-20pt]{0pt}{8pt}$であるから

$$\{\framebox[2.5cm]{\rm (1)}\bigm \vert m,n\in \mathbb{Z}\}\strut\subseteq \mathbb{Z}\rule[-20pt]{0pt}{8pt}$$

である．逆に， $\mathbb{Z}\subseteq\{\framebox[2.5cm]{\rm (1)}\bigm \vert m,n\in \mathbb{Z}\}\rule[-20pt]{0pt}{8pt}$を示す． $\ell\in \mathbb{Z}\strut$を任意の整数とする．

$$\framebox[6cm]{\rm (2)}\rule[-20pt]{0pt}{8pt}$$

を示せば良い． $ax+by=1\strut$をみたす整数$x,y$が存在するから，$m$として$\ell x$，$n$として $\ell y\strut$を考えると，

$$ma+nb=\framebox[2.5cm]{\rm (3)}=\ell\rule[-20pt]{0pt}{8pt}$$

となり， $\framebox[6cm]{\rm (2)}\rule[-20pt]{0pt}{8pt}$が示される．

問題 1.48   $p>1$を自然数とする． $\{m\in \mathbb{Z}\bigm \vert m-1$は$p$で割り切れる$\}\strut$ $=\{pn+1\bigm \vert n\in\mathbb{Z}\}\strut$ を示せ．

$A\ne B\strut$を証明するには定義より $A\nsubseteq B$または $B\nsubseteq A$を示せば良い．

$A \subsetneqq B$を証明するには， $A\subseteq B \wedge B\nsubseteq A$ を示せば良い．

例題 1.49   $\{4n^2+4n+4 \bigm \vert n \in \mathbb{Z}\}\strut\subsetneqq \{m^2+3\bigm \vert m \in \mathbb{Z}\}\strut$を示せ．

解： 問題1.37と問題1.41より示される． $\Box$

問題 1.50   次を示せ．

1. $\{n^2+n \bigm \vert n \in \mathbb{Z}\}\strut\subsetneqq \{2m\bigm \vert m \in \mathbb{Z}\}\strut$
2. $\{9p^2+6p+2 \bigm \vert p \in \mathbb{Z}\}\strut\subsetneqq \{m^2+1\bigm \vert m \in \mathbb{Z}\}\strut$
3. $\{4n^2+6n+2 \bigm \vert n \in \mathbb{N}\}\strut\subsetneqq \{m^2+m\bigm \vert m \in \mathbb{N}\}\strut$
4. $\{n(n+1)(n+2) \bigm \vert n \in \mathbb{Z}\}\strut\subsetneq \{6m\bigm \vert m \in \mathbb{Z}\}\strut$